今回は、2進数の計算方法(足し算・引き算・シフト演算)についての解説です。
1. 足し算
まずは、なじみのある10進数の考え方でおさらいしてみましょう。
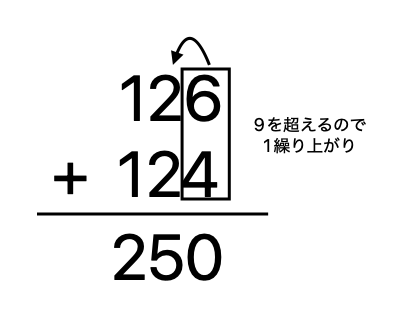
10進数の場合、一つの桁(箱)に入る数字は「9」までです。
上記の式で言うと、1の位は合計が10になるため、あふれて次の位に「1」繰り上がりします。
これを踏まえて計算すると、答えは250となります。
では、2進数になるとどうなるでしょうか?
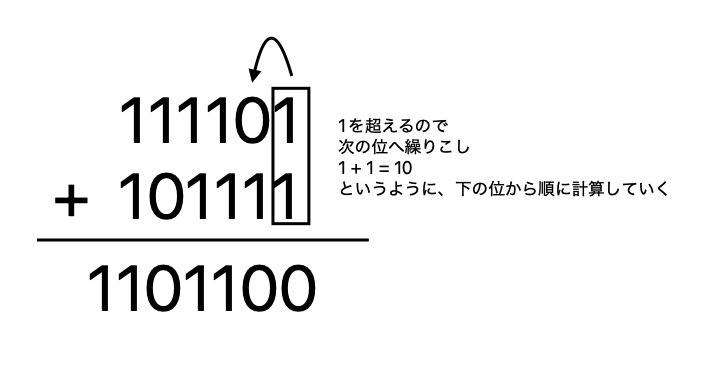
2進数の場合、一つの桁(箱)に入る数字は「1」までです。「2」になった時点で桁あふれします。
上記の式で言うと、1の位は合計が2になるため、次の位に繰り上がりします。
同様のルールで次の位の計算を進めていくと、答えは1101100となります。
2. 引き算(補数表現)
実は、コンピュータは「足し算」しかできません。
そこで、引き算を足し算の形で処理するために考え出されたのが「補数表現」です。
10進数の補数
「引く」代わりに「足すと桁上がりしてゼロに戻る数」を使います。
(例)3桁の数字「123」に対する補数
- あといくつ足せば繰り上がりせず最大値(999)になるか? → 876(9の補数)
- あといくつ足せば繰り上がりするか(1000になるか)? → 877(10の補数)

2進数の補数
2進数でも考え方は同じです。ビットを反転させるのがポイントです。
(例)4桁の2進数「0011」に対する補数
- あといくつ足せば最大値(1111)になるか? → 1100(1の補数:ビット反転)
- あといくつ足せば繰り上がりするか? → 1101(2の補数:+1する)

3. 論理シフト
論理シフトとは、ビット列を左右にズラす際、「符号(プラス・マイナス)を一切気にせず、空いた場所に必ず『0』を入れる」やり方です。
画像処理やフラグ管理など、符号のないデータを扱う際に使われます。
基本的なルールは以下の通り、非常にシンプルです。
-
すべてのビットをそのまま指定された方向にズラす。(符号ビットも特別扱いしません)
-
空いたスペースには常に
0を入れる。
ポイント: 「算術シフト」とは異なり、符号ビットの保護やオーバーフローを気にする必要はありません。「空いたら0を埋める」と覚えればOKです。
8ビットの2進数 1100 1010 を例に実際に計算してみましょう。
① 論理「左」シフト
すべてのビットを左にずらし、右側の空いた場所に0を入れます。
- 元の値:
1100 1010 - 左シフト後:
1001 0100
※左端の1は押し出されて消え、右端には0が補充されます。
② 論理「右」シフト
すべてのビットを右にずらし、左端の空いた場所に0を入れます。
- 元の値:
1100 1010 - 右シフト後:
0110 0101
※右端の0は押し出されて消え、左端には0が補充されます。
今回のまとめ
| 用語 | 意味・ポイント |
|---|---|
| 2進数の足し算 | 「2」になったら隣の桁へ繰り上がりする |
| 補数(2の補数) | 引き算を足し算で行うための表現。「反転して+1」で作れる |
| 論理シフト | 符号を無視してビットをズラすこと。空いた場所は必ず「0」 |
| 論理シフトの用途 | 画像データや符号なし整数の倍数・除算計算など |
