今回は、前回の論理演算についての続きの内容となります。
1.ベン図(続き)
– NAND(否定論理積)
どちらも1のとき、0を出力するという考え方
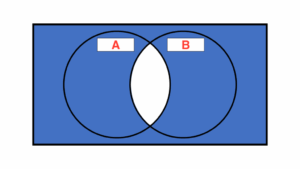
真理値表
| A | B | 出力 |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
– NOR(否定論理和)
どちらかが1のとき、0を出力するという考え方
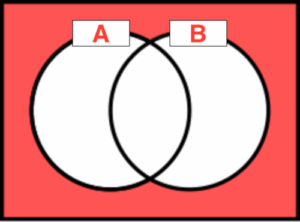
真理値表
| A | B | 出力 |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
– XOR(排他的論理和)
どちらかが1の時、1を出力する
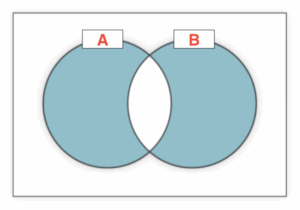
真理値表
| A | B | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
では、これまでの論理を使って、二進数を表すとしたら、どの方法が良いのか?
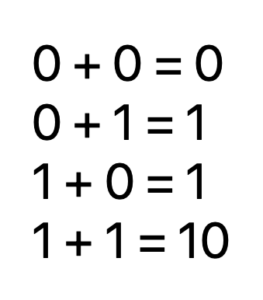
XOR真理値表
| A | B | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
つまり、XOR論理を使用すると、できるという事となる。
今回のまとめ
| 用語 | 意味 |
|---|---|
| NAND(否定論理積) | どちらも1のとき、0を出力するという考え方 |
| NOR(否定論理和) | どちらかが1のとき、0を出力するという考え方 |
| XOR(排他的論理和) | どちらかが1の時、1を出力する |
| 2進数はどれを使うか? | XOR真理値表 |
